假设检验的p值

检验之星

检验统计量及其抽样分布

为了更好地理解假设检验的p值，首先回顾一下检验统计量及其抽样分布。
统计量可定义为不含有任何总体未知参数的样本函数。如下将以正态分布的数学期望 \mu 的假设检验 H_0\!:\mu=\mu_0 为例说明统计量、检验统计量以及抽样分布。
称来源于正态总体 X\sim N(\mu,\sigma^2) 的 n 个相互独立的随机变量 X_1，\cdots,X_n 为容量为 n 的样本( n 个随机变量的集合为样本，每个随机变量均为元素)。为了进行统计分析和推断，需要归纳和提炼样本中的统计信息从而生成了统计量，例如样本均值\bar X 和方差 S^2，
\bar X\!=\!\dfrac{1}{n}\!\sum\limits_{i=1}^nX_i ， S^2\!=\!\dfrac{1}{n\!-\!1}\sum\limits_{i=1}^n(X_i\!-\!\bar X)^2
均为样本的函数且不包含未知总体参数\mu 或 \sigma^2 ，因而均为统计量。如果获取了样本X_1，\cdots,X_n的一组观测值(称之为样本值)，x_1，\cdots,x_n，则可以求出统计量\bar X 和 S^2的对应值 \bar x 和 s^2，方法如下，
\bar x\!=\!\dfrac{1}{n}\!\sum\limits_{i=1}^nx_i ，s^2\!=\!\dfrac{1}{n\!-\!1}\sum\limits_{i=1}^n(x_i\!-\!\bar x)^2
可见如果包含了未知参数则无法计算\bar x 和 s^2。此处用大写字母代表随机变量，例如X_1，\cdots,X_n，\bar X 和 S^2等；用小写字母代表随机变量的观测值，例如x_1，\cdots,x_n，\bar x 和 s^2等。
统计量的统计分布称为抽样分布。例如可以证明\bar X\sim N\!\left(\mu,{\sigma^2}/{n}\right)， \frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n\!-\!1) 。抽样分布代表了在重复对样本X_1，\cdots,X_n进行观测并计算统计量时(例如\bar X)，统计量所表现出来的统计分布规律。例如从一片森林中随机抽取10样木测量树高，并求平均树高。如果重复地随机抽取10株并求平均树高时，可以获得一系列各不相同的平均树高，所有平均树高表现出了的统计规律可视为平均树高的抽样分布。
检验统计量可定义为仅包含待检验的总体参数，且其抽样分布不包含任何未知参数的统计量。虽然检验统计量包含待检验的未知总体参数，但在假设为真时未知参数可取所假设的值，同样可视为不包含任何未知总体参数。从\bar X 的抽样分布可有，
\dfrac{\bar X-\mu}{\sqrt{\sigma^2/n}}\sim N(0,1)
上式的抽样分布不包含任何未知参数( \mu=0， \sigma^2=1)，但左侧表达式不仅包含了待检验的参数 \mu ，还包含了总体方差\sigma^2 。如果 \sigma^2未知，则(\bar X\!-\!\mu)/\!\sqrt{\sigma^2\!/n} 并非一个检验统计量。
由于\bar X 和 S^2 相互独立，根据 t 分布的定义可有
T=\dfrac{\bar X-\mu}{\sqrt{S^2/n}}\sim t(n-1)
上式左侧仅包含了待检验的参数 \mu；而 \bar X 和 S^2为统计量，在获取样本的一次观测后即可计算二者的值；n 为已知的样本容量。不仅如此，其抽样分布不包含任何未知参数，因而(\bar X\!-\!\mu)/\!\sqrt{S^2\!/n} 为一个检验统计量。
顾名思义，检验统计量可用于决定拒绝或接受统计假设。此处"接受假设"说法并不准确，应该表述为"无法拒绝假设"，但由于"接受假设"更为通俗易懂而采用了此说法。
例如对于统计假设 H_0\!:\mu=\mu_0，在假设为真时，
T=\dfrac{\bar X-\mu_0}{\sqrt{S^2/n}}\sim t(n-1)
在获取一个样本值x_1，\cdots,x_n时，可求出相对应的检验统计量 T 对应观测值 t_0 ，即 t_0\!=\!{(\bar x\!-\!\mu_0)}/{\!\sqrt{s^2\!/n}} (注意\mu_0为假设值，常设定为0或一个已知量)。求出 t_0 后，可根据预定的显著性水平 \alpha 和自由度 n\!-\!1 查t分布表确定临界值，并根据t_0和临界值的对比关系拒绝或接受假设。此为关于统计假设H_0\!:\mu=\mu_0的 t 检验。
除了一般的假设检验方法外，还有区间估计法(如果假设的参数值 \mu_0 落在置信区间之外，则拒绝统计假设H_0\!:\mu\!=\!\mu_0)和 p 值法。
简单地说，p 值为依据 t_0值和抽样分布而确定的一个概率值， 如果\boldsymbol{p}值小于显著性水平 \boldsymbol{\alpha} 则拒绝假设，否则接受假设。
假设检验的p值

p 值为一个概率值，因而其值介于0-1之间。假设依据手中样本值求出检验统计量的值为 t_0，则 p 值代表了在假设为真时，如果在同等条件下重复进行试验，获取比 t_0 更为极端的检验统计量的概率。此处"更为极端"的意义为在距离上"更加远离接受区域"，或者等价地"更加接近拒绝区域"，因而此处"极端"的意义取决于假设检验类型。
单侧检验的p值

如果假设检验为左侧检验，即拒绝区域位于抽样分布的左侧，仅将趋近于左侧的程度视为"极端"的尺度。图(1)中红点代表了t_0，曲线代表了检验统计量的抽样分布。红点左侧的检验统计量均比 t_0更接近左侧的拒绝区域，因而蓝色区域(面积)代表了p 值，即 p(T\!\le\!t_0) 值；而右侧检验则恰好相反，绿色区域代表了右侧检验的 p 值，即 p(T\!\ge\!t_0)值 。



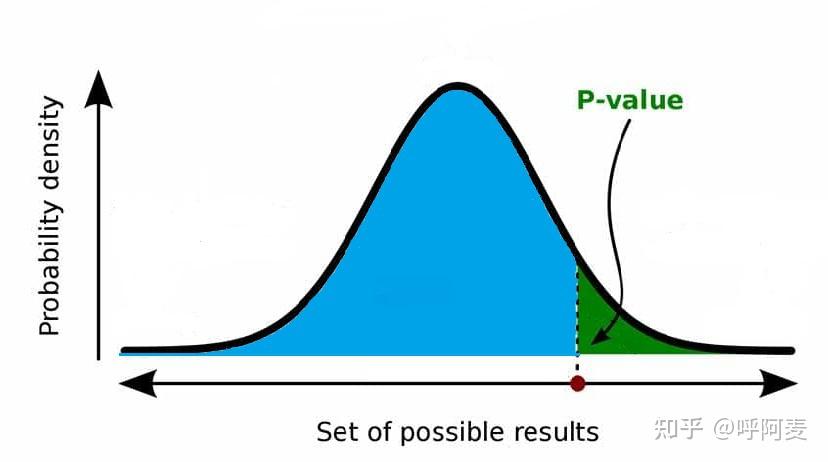
图(1)--图中的红点为检验统计量值t0；如果为右侧检验，则对应的p值为绿色区域代表的概率；如果为左侧检验，则p值为蓝色区域代表的概率。

对称抽样分布的双侧检验p值

为易于理解，双侧检验先考虑抽样分布以0轴对称的情形，主要为 t 检验。由于两侧都有拒绝区域，不可认为图(1)的蓝色区域对应于左侧拒绝区域 p 值，绿色对应于右侧的 p 值。图(1)中红点 t_0 到其0轴间(曲线峰值处)任何一点均不如 t_0 极端；不仅如此，由于&#34;更为极端&#34;的意义为在距离上&#34;更加接近接受区域&#34;，因而所有 <\!-t_0 的检验统计量也在左向上比 t_0 更为极端，如图(2)中左侧竖线的左侧所有点。图(2)中红点依然代表了 t_0，而左侧的绿色竖线则为 t_0关于0轴对称的 -t_0 点，2条竖线间任何一点均不如 t_0 极端，而2个绿色区域的任何一点均比 t_0 极端。因而对于双侧检验，p 值为2个绿色区域之和。
给定一个 t_0 值，如果 t_0>0 则 p 值等于 p(T>t_0)+p(T<\!-t_0) ，而且由于抽样分布的0轴对称性， p(T<\!-t_0)=p(T>t_0) ，所以 p 值等于 2p(T>t_0) ；如果 t_0<0 ，则 p 值等于 2p(T>|t_0|) ；综合两种情形，可有p 值等于
pv=2p(T>|t_0|)



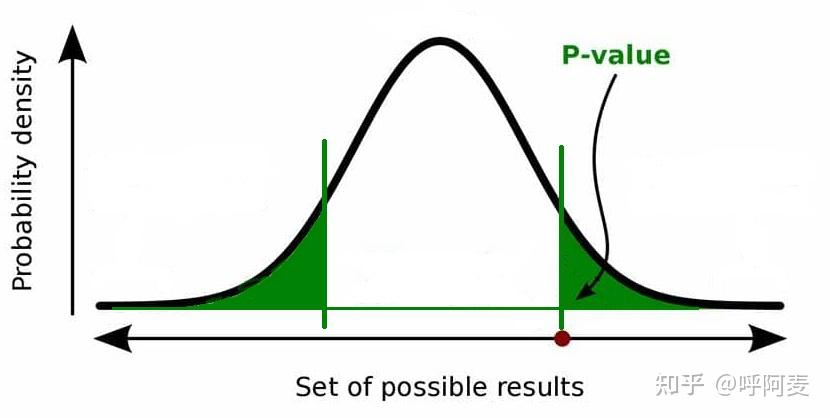
图(2)--如果为双侧检验，由于红点更接近右侧的拒绝区域，因而右侧绿色区域代表了在右侧方向上的p值；因而，在左侧方向上也应有一个向左侧方向的等量p值，对应左侧的绿色区域。

非对称抽样分布的双侧检验p值

如果抽样分布为非对称分布，例如F分布和 \chi^2分布，双侧检验的 p 值可表示为
p_v=2\!\times\! \min\!\underline{\big[p(T\le t_0),\:p(T\ge t_0)\big]}
此处min[,]为取最小值的函数。
图(3)中曲线为F分布的概率密度曲线(分子和分母自由度分别为15和20)，红色竖线代表了依据手中样本计算出的检验统计量值 t_0。图(3)绿色区域的所有点均比 t_0 更为极端，而蓝色区域并非如此；既包含了不如 t_0的点，也包含了在左侧方向上比 t_0 更为极端的点。图(4)将图(3)的蓝色区域分为2个部分，其中两条红色竖线间蓝色区域的所有点均不如t_0极端，而左侧的绿色区域则比 t_0 极端。图(4)中左侧的红色竖线代表了 t_0 对应点  t_0^{&#39;}，满足 p(T\le t_0^{&#39;})=p(T\ge t_0) 。由于抽样分布为非对称分布，因而此处的&#34;对应&#34;指概率上的对应，也使 p 值与显著性水平 \alpha 对比结果可用于假设检验。由于 p(T\le t_0)包含了图(4)中左侧绿色区域和蓝色区域，因而有 \underline{\min\!\big[p(T\le t_0),\:p(T\ge t_0)\big]\!=\!p(T\ge t_0)}，而且因为2个绿色区域对应的概率均为p(T\ge t_0), 因而可有如上 p 值表达式。
对于对称的双侧检验，上式同样成立。
可见在同一 \boldsymbol{t}_0 值的前提下，双侧检验的 \boldsymbol{p} 值为单侧检验的2倍。



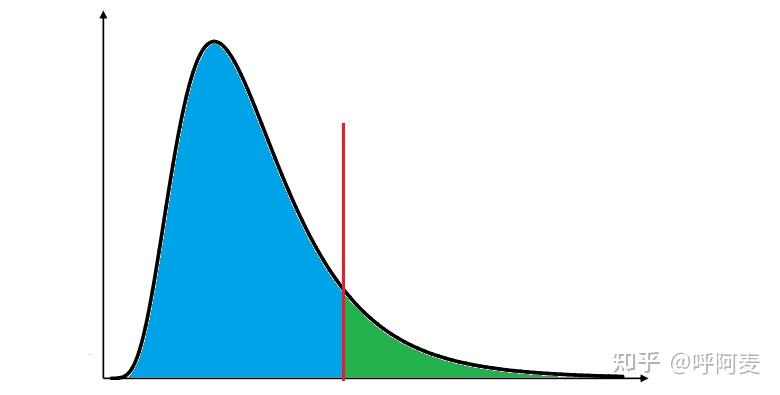
图(3)



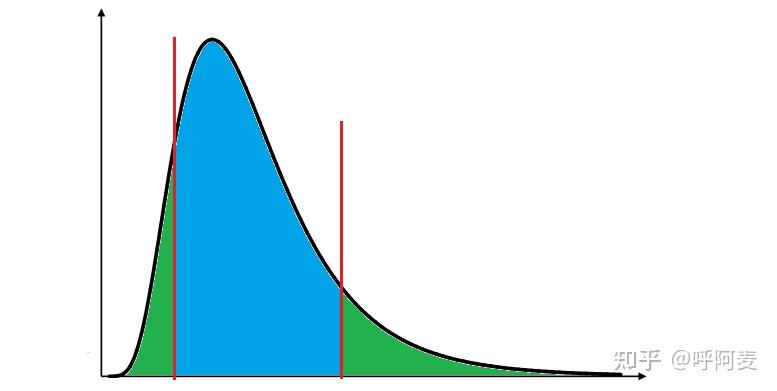
图(4)

假设检验和p值

将 p 值和预定的显著性水平 \alpha 相比，如果 p 值 <\alpha 则拒绝假设。
根据累积分布函数的单调性，可有

• p(X\!<\!a)<p(X\!<\!b)\Longleftrightarrow a\!<\!b ;
  
• p(X\!>\!a)<p(X\!>\!b)\Longleftrightarrow a\!>\!b；
  

左侧检验 p 值等于 p(T\!\le\!t_0)。如果 p 值 <\alpha ，则有{p(T\le t_0)<\alpha}\Longrightarrow  p(T\le t_0)<{p(T\le c_{\alpha})}\Longrightarrow\underline{t_0<c_{\alpha}} (性质1)。此处c_\alpha为左侧检验的临界值，即 p(T\!\le\!c_\alpha)=\alpha。可见当 p 值 <\alpha时， {t_0\!<\!c_{\alpha}}表明检验统计量的值 t_0 落在了拒绝区域。
令c_{1-\alpha}为右侧检验的临界值，即 p(T\!\le\!c_{1-\alpha})\!=\!1\!-\!\alpha，或等价地可有p(T\!\ge\!c_{1-\alpha})\!=\!\alpha。右侧检验 p 值等于 p(T\!\ge\!t_0)。如果 p 值 <\alpha，则有\underline{p(T\!\ge\!t_0)<\alpha}\Longrightarrow \underline{p(T\!\ge\!t_0)<p(T\!>\!c_{1-\alpha})}\Longrightarrow\underline{t_0\!>\!c_{1-\alpha}}(性质2)。可见当 p 值 <\alpha时， t_0 落在了拒绝区域。

对于双侧检验 p 值可表示为，p_v=2\!\times\! \min\!\big[p(T\le t_0),\:p(T\ge t_0)\big]
如果 p_v=2\!\times\! p(T\le t_0) ，则当 p 值 <\alpha时，可有2\!\times\! p(T\le t_0)<\alpha\Longrightarrow p(T\le t_0)<p(T\!<\!c_{\alpha/2}) \Longrightarrow  t_0\!<\!c_{\alpha/2}(性质1)，此处 c_{\alpha/2} 为临界值，有p(T\!\le\!c_{\alpha/2})\!=\!\alpha/2。此时 t_0 落在了左侧拒绝区域，应拒绝假设。
如果 p_v=2\!\times\! p(T\ge t_0) ，则当 p 值 <\alpha时，可有2\!\times\! p(T\ge t_0)<\alpha\Longrightarrow p(T\ge t_0)<\alpha/2  \Longrightarrow p(T\ge t_0)<p(T\!>\!c_{1-\alpha/2}) \Longrightarrow  t_0\!>\!c_{1-\alpha/2}(性质2)，此处 c_{1-\alpha/2} 为临界值，有 p(T\!\le\!c_{1-\alpha/2})\!=\!1\!-\!\alpha/2，或等价地，p(T\!\ge\!c_{1-\alpha/2})\!=\!\alpha/2。此时 t_0 落在了右侧的拒绝区域，应拒绝假设。
可见应在p值小于显著性水平\alpha 时则拒绝假设。
p 值也可以理解为可以拒绝统计假设的最小显著性水平 \alpha 。当以 p 值为显著性水平时，p 值也代表了犯第I类错误的概率，越小的 p 值代表了越小的犯第I类错误的概率，从而倾向于拒绝假设。
如何用excel计算p值

如下的excel函数可用于计算p值，
CHIDIST(x, df)，此处x\!>\!0，df为卡方分布的自由度。此函数返回服从卡方分布随机变量 X 大于 x 的概率，即 p(X\!>\!x)值
FDIST(x, df1, df2)，x\!>\!0，df1和df2分别为F分布的分子自由度和分母自由度。返回 p(X\!>\!x)，此处X为服从F分布的随机变量 。
TDIST(x, df, tails)，要求 x\!>\!0，tails取值为1或2，分别对应单侧检验或双侧检验，df为t分布的自由度。如果 tails=1，则为单侧t检验，TDIST返回 p(X\!>\!x)值，此时返回右侧检验的p值，其中X为服从  t 分布的随机变量。 如果 Tails=2，则为双侧t检验，TDIST函数返回值为 2\!\:p(X\!>\!|x|) 。如果 \boldsymbol{x\!<\!0}，则取 x 的绝对值即可求出对应的 p 值。
例如TDIST(0.98,36,2)=0.3336，TDIST(0.98,36,1)*2=0.3336，FDIST(1.35,2,12)=0.2959
计算示例

有两个水稻品种A和B，各有8个重复，检验二种水稻的产量一致性。

1	2	3	4	5	6	7	8
A	5.310	4.460	5.380	5.460	4.420	4.770	4.650	4.540
B	6.640	5.690	5.630	6.530	4.870	5.110	4.740	4.950

此为独立样本的对比分析问题。两组方差相同与否决定了应采用不同的t检验分析方法，同质方差的独立样本t检验或异质方差的独立样本t检验。此问题包括如下的假设检验

• 方差一致性(同质性)检验的双侧F检验；
  
• 如果F检验结果表明方差一致，则可采用独立样本双侧t检验；
  
• 此问题又可视为单因素方差分析问题，因而可用右侧F检验分析两个样品产量的一致性。
  

(1) 方差同质性的双侧F检验

需要检验A和B两个品种的方差一致性，以确定可采用的t检验方法，等方差t检验或不等方差t检验。
A品种的产量 X_1\sim N(\mu_1,\sigma_1^2) , B品种的产量X_2\sim N(\mu_2,\sigma_2^2)，分别独立地获取容量为 n_1 和 n_2 的样本， X_{11},\cdots,X_{1n_1} 和X_{21},\cdots,X_{2n_2}，样本方差可定义如下，
S_i^2\!=\!\dfrac{1}{n_i\!-\!1}\!\sum\limits_{j=1}^{n_i}(X_{ij}\!-\!\bar X_{i.})^2 ， i=1,2
在统计假设 \sigma^2_1\!=\!\sigma_2^2 为真时，检验统计量T=\frac{S_1^2}{S_2^2}\sim F(n_1\!-\!1,n_2\!-\!1) 。依据备择假设的不同，可有如下3种检验类型，
\begin{array}{c|c|c|l|c} \hline &统计假设&备择假设&拒绝区域&检验类型\\ \hline (a)&\mspace{20mu}H_0：\sigma_1^2=\sigma_2^2\mspace{20mu}&\mspace{20mu}H_a：\sigma_1^2>\sigma_2^2\mspace{20mu}&f>F(n_1\!\!-\!1,n_2\!\!-\!1)_{1-\alpha}&\mspace{20mu}右侧检验\mspace{20mu}\\   (b)&\mspace{20mu}H_0：\sigma_1^2=\sigma_2^2\mspace{20mu}&\mspace{20mu}H_a：\sigma_1^2<\sigma_2^2\mspace{20mu}&f<F(n_1\!\!-\!1,n_2\!\!-\!1)_{\alpha}&\mspace{20mu}左侧检验\mspace{20mu}\\ \hline (c)&\mspace{20mu}H_0：\sigma_1^2=\sigma_2^2\mspace{20mu}&\mspace{20mu}H_a：\sigma_1^2\ne\sigma_2^2\mspace{20mu}&f>F(n_1\!\!-\!1,n_2\!\!-\!1)_{1-\alpha/2}&\mspace{20mu}双侧检验\mspace{20mu}\\  &&&或者&\\ &&&f<F(n_1\!\!-\!1,n_2\!\!-\!1)_{\alpha/2}\\ \hline  \end{array}
在假设检验中称 F(n_1\!-\!1,n_2\!-\!1)_{\alpha} 为临界值，此处下标 \alpha 代表了小于临界值的概率，即p\big[X<F(n_1\!-\!1,n_2\!-\!1)_{\alpha}\big]\!=\!\alpha；也有人用临界值下标代表大于临界值的概率。如果采用此方法时则此处F(n_1\!-\!1,n_2\!-\!1)_{\alpha}需表示为 F(n_1\!-\!1,n_2\!-\!1)_{1-\alpha} 。不同的表示方法截然不同，需注意区分。
以上三种F检验的情形可参考图(5)。图中竖线为临界值，阴影部分为拒绝区域，白色区域为接受区域。



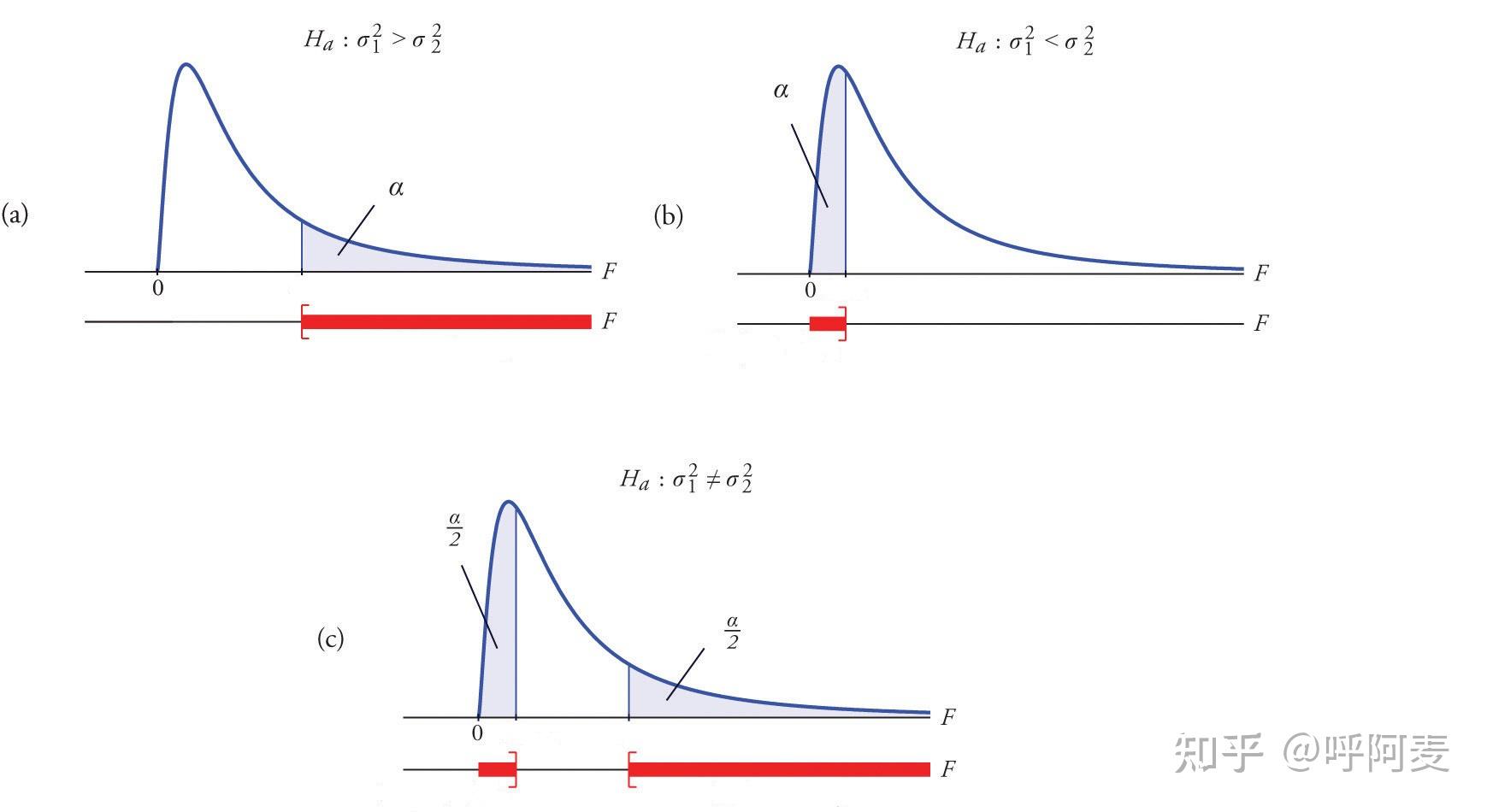
图(5) 图中竖线为临界值，阴影部分为拒绝区域，白色区域为接受区域。

A品种的样品方差值为 s_1^2 =0.1914，B品种为 s_2^2 =0.5485，二者比值为0.3490。由于备择假设为 \sigma^2_1\!\ne\!\sigma_2^2 ，因而需要进行双侧F检验，双侧检验的p值为
2\times \min\!\big[p(T\le t_0),\:p(T\ge t_0)\big] =
=2*MIN(FDIST(0.3490,7,7), 1-FDIST(0.3490,7,7))=0.1882
上式为excel表达式。FDIST(0.3490,7,7)为分子自由度为7，分母自由度为7的F分布随机变量取值大于0.3490的概率，对应于 p(f≥0.3490)，而1-FDIST(0.3490,7,7)代表了p(f≤0.3490)。
(2) 总体数学期望的双侧t检验

由于F检验结果表明两个水稻品种方差一致，因而可采用如下的同质方差t检验法。
有2个总体分别为X_1\!\sim \!N(\mu_1,\sigma^2) , X_2\!\sim\! N(\mu_2,\sigma^2)，各随机抽取容量为 n_1 和 n_2 的样本， X_{11},\cdots,X_{1n_1} 和 X_{21},\cdots,X_{2n_2}，此处X_{ij} 代表了第 i 个总体( i\!=\!1,2 )的第 j 个观测值。样本方差和均值\bar X_1， S_1^2，\bar X_2，S_2^2可分别定义如下，
S_i^2\!=\!\dfrac{1}{n_i\!-\!1}\!\sum\limits_{j=1}^{n_i}(X_{ij}-\bar X_{i.})^2 ，\bar X_{i.}\!=\!\dfrac{1}{n_i}\!\sum\limits_{j=1}^{n_i}\!X_{ij}    (i\!=\!1,2 )
在统计假设 \mu_1\!-\!\mu_2\!=\!0 为真时，可有
T=\dfrac{\bar X_{1.}\!-\!\bar X_{2.}}{\sqrt{S_p^2(1/n_1+1/n_2)}}\sim t(n_1\!+\!n_2\!-\!2)
此处 S_p^2=\dfrac{(n_1\!-\!1)S_1^2\!+\!(n_2\!-\!1)S_2^2}{n_1\!+\!n_2\!-\!2} ，为样本方差以自由度为权重的加权均值，
在获取样本值 x_{11},\cdots,x_{1n_1} 和x_{21},\cdots,x_{2n_2} ，可有检验统计量的值为
t_0=\dfrac{\bar x_1\!-\!\bar x_2}{\sqrt{s_p^2(1/n_1+1/n_2)}} ，
s_p^2=\dfrac{(n_1\!-\!1)s_1^2\!+\!(n_2\!-\!1)s_2^2}{n_1\!+\!n_2\!-\!2} ， s_i^2\!=\!\dfrac{1}{n\!-\!1}\!\sum\limits_{j=1}^{n_i}(x_{ij}-\bar x_{i.})^2 ， \bar x_{i.}\!=\!\dfrac{1}{n_i}\!\sum\limits_{j=1}^{n_i}\!x_{ij} ，
依据手中样本值，可计算
\bar x_1 =4.8738, s_1^2 =0.1914; \bar x_2 =5.5200, s_2^2 =0.5485, s_p^2 =0.3699， n_1\!=\!n_2\!=\!8 ,
检验统计量值 t_0 =(4.8738-5.5200)/sqrt(2*0.3699/8)=-2.1250
检验统计量-2.1250对应的p值为
p_v=2\!\times\! p(T\ge |t_0|) =2*TDIST(2.1250, 14, 1)=0.0519
也可以用=TDIST(2.1250, 14, 2)获得一样的结果。
(3) 总体数学期望的左侧F检验

此问题可视为试验因子仅有2个水平(A和B)的单因素方差分析问题。
如果一个试验因子，共计有 a 个水平，每个水平均有 n 个重复，第 i 个水平的第 j 个观测值记为X_{ij}，且有X_{ij}\!\sim\! N(\mu_i,\sigma^2) ，即各水平的数学期望依次为 \mu_1,\cdots,\mu_a ，方差一致均为 \sigma^2 。在统计假设 \mu_1=\cdots=\mu_a 为真时，可有
T=\dfrac{n\sum_{i=1}^{a}(\bar X_{i.}\!-\!\bar X_{..})^2\big/(a\!-\!1)}{\sum_{i=1}^{a}\!\sum_{j=1}^{n}(X_{ij}\!\!-\bar X_{i.})^2\big/(an\!-\!a)}\sim F(a\!-\!1,an\!-\!a)
此处\bar X_{i.}\!=\!\dfrac{1}{n}\sum\limits_{j=1}^n\!X_{ij}，\bar X_{..}\!=\!\dfrac{1}{an}\sum\limits_{i=1}^a\sum\limits_{j=1}^n\!X_{ij}，
上式中分子项即为组间离差平方和同其自由度的商(组间离差均方)，分母项为组内离差平方和同其自由度的商(均内离差均方)

离差平方和	自由度	离差均方	F检验值	p值
水稻品种	1.6706	1	1.6706	4.5160	0.0519
误差	5.1790	14	0.3699
合计	5.1969	15

F检验值在统计假设\mu_1,\cdots,\mu_a为真时大约等于1，F检验值越大越倾向于表明\mu_1,\cdots,\mu_a为假，而备择假设(至少有一对数学期望不等)为真，因而方差分析仅做右侧F检验。p值=FDIST(4.5160, 1, 14)=0.0519。F检验和t检验的p值一致，均为0.0519，t检验值(-2.1250)的二次方等于F检验值4.516。独立样本的t检验和F检验存在如此对应关系。
(4) SAS分析

如下SAS代码可用于完成本示例中(1)-(3)的所有统计分析。
data rice;
do rep=1 to 8;
   do group=&#34;A&#34;,&#34;B&#34;;
      input y@@;
      output;
   end;
end;
cards;
5.31        6.64
4.46        5.69
5.38        5.63
5.46        6.53
4.42        4.87
4.77        5.11
4.65        4.74
4.54        4.95
;
proc ttest data=rice;
   class group;
   var y;
run;

proc glm data=rice;
   class group;
   model y=group;
run;参考文献

TDIST 函数
The meaning of two sided (double tailed) p-values
p-value Calculator


原文地址：https://zhuanlan.zhihu.com/p/679023158