LLM高效推理之P/D分离：研究动机

营养师 · 发表于 2025-4-24 16:28

登陆有奖并可浏览互动！

您需要登录才可以下载或查看，没有账号？立即注册

×

本文将探讨大模型推理加速领域的一个新兴研究方向：Prefilling/Decoding 分离技术。受限于文章篇幅，本次讨论将聚焦于该领域的研究动机，主要基于 Roofline 工具展开理论分析，并介绍 DistServe 论文的关键实验发现。具体的解决方案与优化策略将在后续系列文章中进行深入探讨。
问题背景

大语言模型目前常用 decoder-only 架构，推理过程在逻辑上可分为两个阶段：Prefilling（预填充阶段）和 Decoding（解码阶段）。其中，Prefilling 并行处理所有输入 token（包括 RAG 检索到的文档片段、System Prompt 和 User Prompt 等），存储计算得到的 Key-Value 激活值（即 KV Cache）并生成首个输出 token。Decoding 则利用 KV Cache 自回归地（上一位置的输出作为下一位置的输入）生成新的 token，并将计算产生的新 KV 追加到 Cache 中。
Prefilling 阶段主要优化从请求输入到生成首个 token 的时间延迟（Time To First Token, TTFT），而 Decoding 阶段则着重优化连续 token 之间的生成间隔（Time Per Output Token, TPOT）。以对话系统为例，较低的 TTFT 能确保快速响应，而 TPOT 只需略高于人类阅读速度即可。然而，当这两个过程在计算设备上并行执行时，往往难以同时满足两者的性能需求。
Prefilling 阶段属于计算密集型（compute-bound）任务，而 Decoding 阶段则呈现访存密集型（memory-bound）特征。这种计算特性的差异导致：在边缘设备等计算能力受限的环境中，Prefilling 性能会受制于硬件算力；而在配备 DGX/HGX 等高性能计算单元的云端服务器上执行 Decoding 时，则会造成计算资源利用率低下。值得注意的是，增大 batch size 虽能有效提升 Decoding 阶段的访存效率进而提高吞吐量，但对 Prefilling 阶段的性能提升效果有限，这进一步印证了两个阶段需要采用差异化的优化策略。
这个关于 bound 的结论是如何得到的呢？
理论分析

下面，我们用 Roofline Model[1]给出一个粗糙的定量分析：定义 \pi 和 \beta 分别为计算设备的最大计算能力（FLOP/s）和最大存储传输带宽（Byte/s），定义推理过程的计算量除以访存量为计算强度 I （FLOP/Byte）。当计算强度低于 \pi/\beta 时，性能瓶颈主要来自于访存能力，反之来自于计算能力。Roofline Model 不是用来衡量模型的效率，而是衡量模型独占设备时对资源的利用率，这将指导模型选用多强的设备，设备支撑多大的模型，避免出现“大炮打蚊子”的资源浪费。
Prefilling 阶段的计算强度

对于 Attention 层，假设输入 batch size 为 b，序列长度为 n，模型隐层维度为 d，注意力头数为 m，GQA 的组数为 g 。那么，计算 Q、K、V 矩阵的时间复杂度为 3bnd^2，对 Q 和 K 进行 RoPE 编码需要 bnd+bnd/g ，计算 QK^\top需要 bn^2d，softmax 需要 3bmn^2，其结果与 V 相乘需要 bn^2d，再乘以一个输出投影矩阵需要 bnd^2 。而对于空间复杂度，存储模型参数需要 2d^2+2d^2/g ，存储中间激活需要 3bnd+bmn^2。可以得到 Prefilling 阶段的 Attention 的计算强度为 \frac{bnd(4d+1+1/g+2n)+3bmn^2}{2d^2+2d^2/g+bn(3d+mn)} 。
对于 FFN 层，假设升维后的维度为 4d。那么，升维过程的时间复杂度为 8bnd^2，Swish 激活函数需要 8bnd，Hadamard 积需要 4bnd ，降维过程需要 4bnd^2 。对于空间复杂度，存储模型参数需要 12d^2，存储中间激活需要 8bnd。可以得到 Prefilling 阶段的 FFN 的计算强度为 \frac{3bn(d+1)}{3d+2bn} 。
Decoding 阶段的计算强度

当计算到第 t+1 个输出 token 时：
对于 Attention 层，假设输入 batch size 为 b，模型隐层维度为 d，注意力头数为 m，GQA 的组数为 g 。计算 Q 及其 RoPE 编码的时间复杂度为 bd^2+bd ，K、V 矩阵直接从 cache 中获取，无需计算。计算 QK^\top需要 b(n+t)d，softmax 需要 3bm(n+t)，其结果与 V 相乘需要 b(n+t)d，再乘以一个输出投影矩阵需要 bd^2 。而对于空间复杂度，存储模型参数需要 2d^2+2d^2/g ，存储中间激活需要 bd+2b(n+t)d+bm(n+t)。可以得到 Decoding 阶段的 Attention 的计算强度为 \frac{b(d+(n+t)(2d+3m)+2d^2)}{2d^2+2d^2/g+bd+b(n+t)(2d+m)} 。
对于 FFN 层，假设升维后的维度为 4d。那么，升维过程的时间复杂度为 8bd^2，Swish 激活函数需要 8bd，Hadamard 积需要 4bd ，降维过程需要 4bd^2 。对于空间复杂度，存储模型参数需要 12d^2，存储中间激活需要 8bd。可以得到 Decoding 阶段的 FFN 的计算强度为 \frac{3b(d+1)}{3d+2b} 。
计算强度对比分析

对于 FFN 层，易得 \frac{3b(d+1)}{3d/n+2b}\geq \frac{3b(d+1)}{3d+2b}，即 Prefilling 阶段的计算强度更大。在实际推理时，由于显存受限，往往是 d\gg b，而 n 通常是 1k 以上的数量级，所以这两个计算强度相差甚远。Attention 层的结果与之类似。为了清晰地对比二者，我们以 LLaMA2-7B 的模型结构为例，考虑 NVIDIA RTX 3090 作为计算设备，绘制 Roofline 图。
LLaMA2-7B 共有 m=32 个注意力头，隐层维度 d=4096，使用 MHA 所以 g=1[2]。考虑 Prefilling 的输入长度为 1k，Decoding 的当前输出 token 为第 1k 个，batch size 为 1（其他参数区别不大）。NVIDIA RTX 3090 的 Float32 理想计算能力大致为 35.58 TFLOPS，HBM（显存）的读写速度平均为 0.936 TB/s[3]。Roofline 图如下所示，横纵坐标都是 log scale。

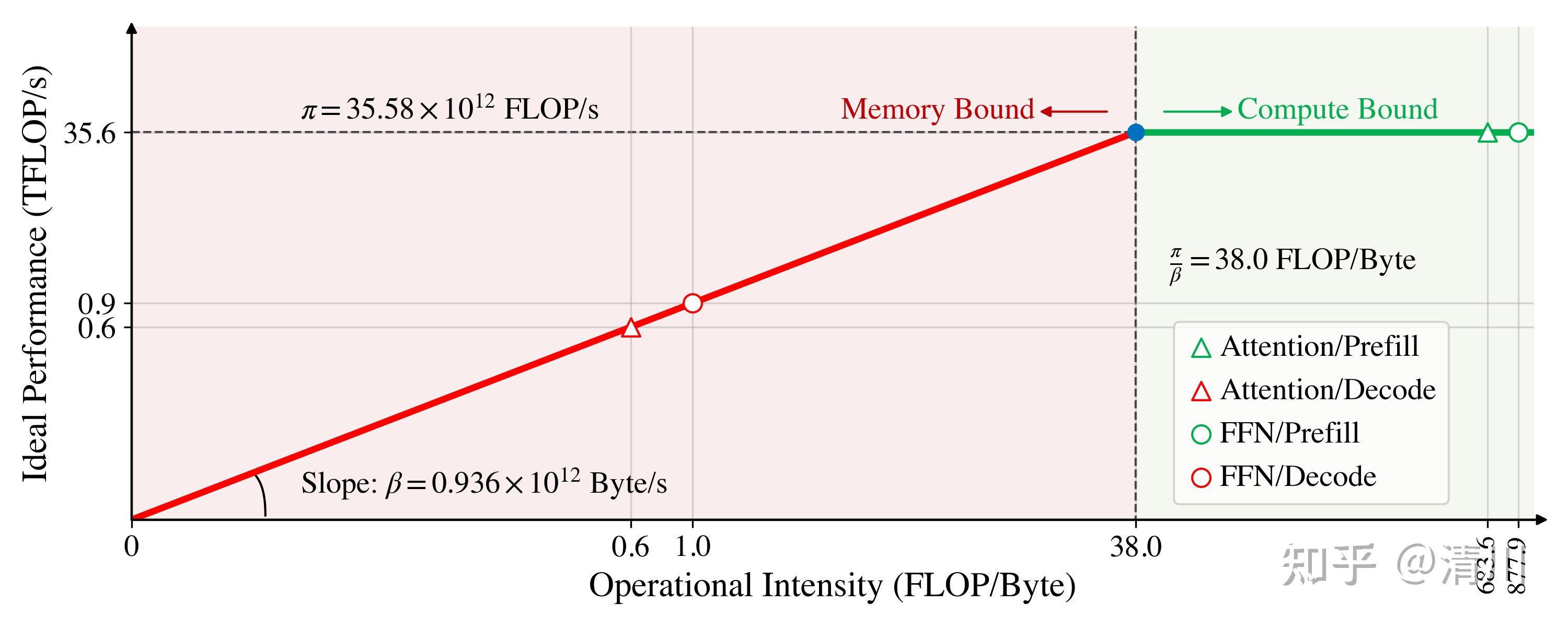
LLaMA2-7B 在 NVIDIA RTX 3090 上的 P/D 阶段瓶颈分析

显然 Decoding 阶段都落在了 Memory Bound 区域，而 Prefilling 都落在 Compute Bound 区域。这和定性分析的结果是一致的：Decoding 阶段受到自回归逻辑的限制，每次只能计算一个 token，却依赖之前所有的 KV 值；而 Prefilling 过程虽然也要存储所有的 KV，却同时计算了所有输入 token，提高了计算强度。
注意这里我们假定的是 SRAM 很小，每次计算都要从 HBM 中加载参数或向 SRAM 写入激活值。同时假定了 HBM 大小不成为瓶颈，一旦其存储大小受限，我们就得考虑将部分参数和激活卸载到 CPU Memory，那么等效的读写带宽就会更小，上图红色线段就会呈现出更小的斜率，从而造成更大面积的 Memory Bound 区域。
实验分析

DistServe: Disaggregating Prefill and Decoding for Goodput-optimized Large Language Model Serving 是 2024 年发表在 OSDI 上的 P/D 分离的开山之作，在论述分离架构的优势时，直接举了个例子：在 A100/80G 上推理 13B 大模型（batch size 为 512，输出长度为 64），只推理 Prefilling 阶段或只推理 Decoding 阶段时，支持的最高并发请求数量明显优于现有主流推理系统（如 PagedAttention[4]、Orca[5]等）。现有系统普遍采用 P/D 一体化设计架构，如 Orca 的 Continuous Batching 技术，为了最大化系统吞吐率，将处于不同推理阶段、不同序列长度和解码位置的请求合并处理。

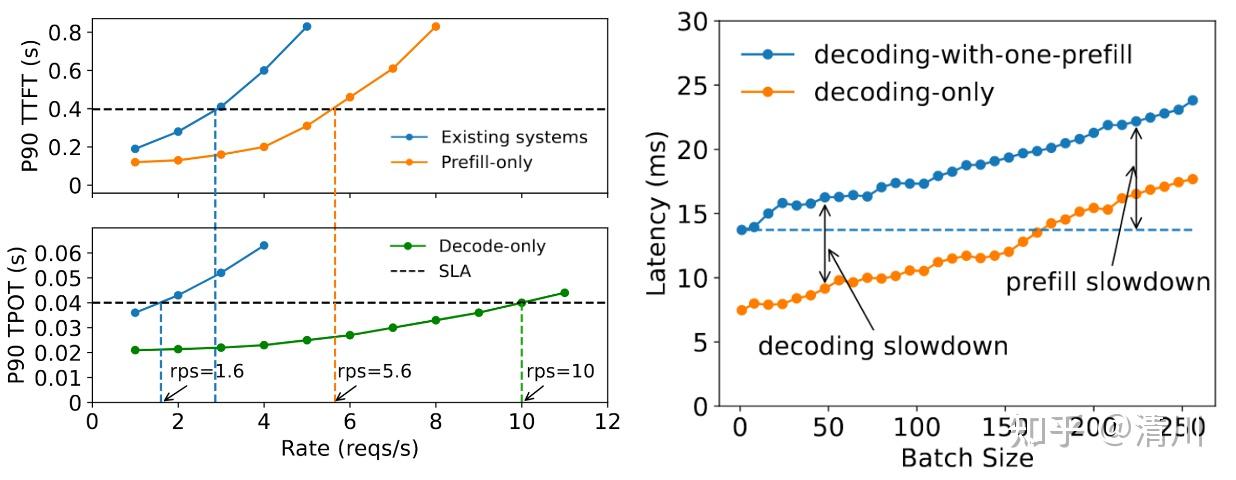
DistServe 绘制了如左图所示的不同情况下的服务质量曲线。纵坐标 P90 表示 90% 的请求满足服务等级协议（SLA）要求，其中黑色虚线标注了示例 SLA 的具体指标：要求 90% 请求的 TTFT ≤ 0.4s，TPOT ≤ 0.04s。曲线与 SLA 阈值的交点横坐标表征了系统在保证服务质量前提下的最大并发处理能力。
实验数据表明，当计算设备专用于 Prefilling 或 Decoding 时，系统支持的并发请求量显著提升，这意味着 MaaS（Model as a Service）提供商可以借此优化资源配置，显著降低运营成本。
右图进一步探讨了在批量进行的 Decoding 中加入一条 Prefilling 请求造成的影响。Prefilling 因为 Decoding batch size 从 0 逐渐增加而总的延迟上升，decoding 也因为加入了一条 Prefilling 从橘色线跳到了蓝色线。当输入长度从 128（当前右图的设定）增长到 1024 时，Decoding 过程的延迟上升更加明显。
研究展望

以上分析并不能说明 P/D 分离一定好，但至少给出了一个愿景。但在实际应用中，Prefilling 设备和 Decoding 设备之间的 KV Cache 传输开销可能造成很大的 overhead。另外，像后面 Kimi 的 Mooncake[6]讨论的那样，这种 P/D 分离架构主要在长序列的情况下有效。如果在本文上面给出的理论分析中代入 n=64，并将计算设备换成 A100[7]，就会发现两个阶段的计算强度都落入了 Memory Bound，这时可能需要增大 batch size 来进行补偿。
有些人质疑 P/D 分离，认为大模型的场景也不都是长序列的。但因为我本身更关注 RAG，它依赖来自文档库或者搜索引擎的长文本做 in-context 增强，所以在其位、谋其政。我觉得 P/D 分离对于 RAG 来说是好事，甚至可以把 Retrieval 和 Prefilling 绑定在一起，把 Decoding 解耦出去，产生专门做 KDN（Knowledge Delivery Network[8]，类似 CDN）服务的公司。
这些 KDN 公司可以为企业和高校做 RAG 解决方案，把专用的、隐私的文档以及常用的互联网内容进行切片、索引和 Prefill，用户在手机或者 PC 上只需要连入企业网、校园网，就可以即插即用地访问这些知识。在高性能服务器上统一 Prefill，不断同步到分布式的存储节点上，然后多客户端检索复用，这样既避免在弱设备上 Prefill，又节省了服务器 Decoding 的成本（成本卸载到用户侧）。那些 MaaS 公司也可以从这种 KDN 上订阅服务，这样自己只做 Decoding，对用户的服务计费也变得清晰、透明了。
我最近的一篇工作（Efficient Distributed Retrieval-Augmented Generation for Enhancing Language Model Performance）对这种端云分布式 RAG 架构进行了探讨，之后大概率会沿着这个方向继续前进。
参考